Scroll:practical Geometry >> tangent of the circle >> ps (4156)
Written Instructions:
For each Multiple Choice Question (MCQ), four options are given. One of them is the correct answer. Make your choice (1,2,3 or 4). Write your answers in the brackets provided..
For each Short Answer Question(SAQ) and Long Answer Question(LAQ), write your answers in the blanks provided.
Leave your answers in the simplest form or correct to two decimal places.
| 1) Draw a circe of radius 3cm. From an external point 7cm away from its centre, construct the pair of tangents to the circle and measure their lengths. Answer:_______________ |
| 2) Construct a ►PQR in which the base PQ = 6cm, ∠R = 60 ° and the altitude from R to PQ is 4cm Answer:_______________ |
| 3) Draw a circle of radius 3.2cm. At a point P on it, draw a tangent to the circle using the tangent -chord therem.
Answer:_______________ |
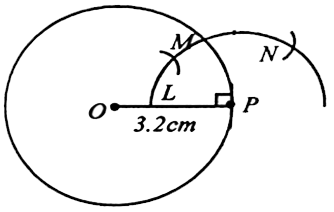
| 4) Draw a circle of radius 3.2cm. Take a point P on this circle and draw a tangent at P. (using the centre).
Answer:_______________ |
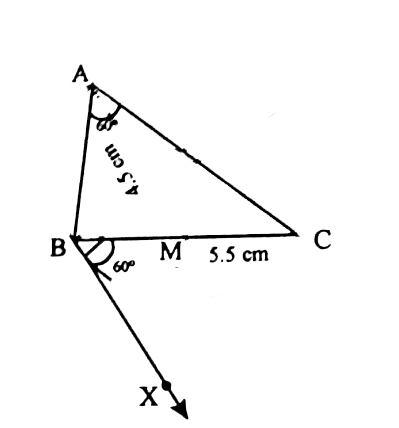
| 5) Construct a ► ABC in which BC =5.5cm.<A = 60 °. And the median AM from vertex aA is 4.5cm. Answer:_______________ |
| 6) Draw a circe of radius 3cm. From an external point 7cm away from its centre, construct the pair of tangents to the circle and measure their lengths. Answer:_______________ |
| 7) Construct a ►PQR in which the base PQ = 6cm, ∠R = 60 ° and the altitude from R to PQ is 4cm Answer:_______________ |
| 8) Draw a circle of radius 3.2cm. At a point P on it, draw a tangent to the circle using the tangent -chord therem.
Answer:_______________ |
| 9) Draw a circle of radius 3.2cm. Take a point P on this circle and draw a tangent at P. (using the centre).
Answer:_______________ |
| 10) Construct a ► ABC in which BC =5.5cm.<A = 60 °. And the median AM from vertex aA is 4.5cm. Answer:_______________ |
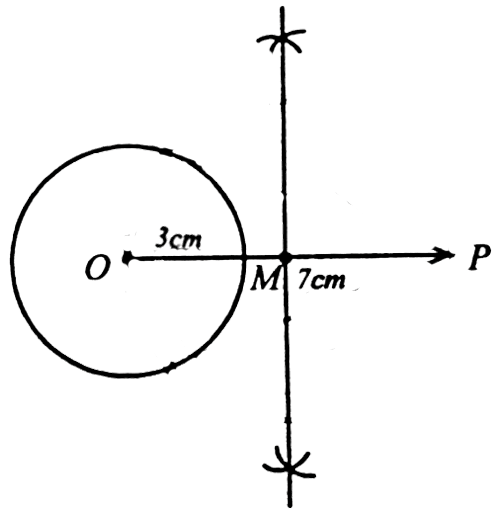
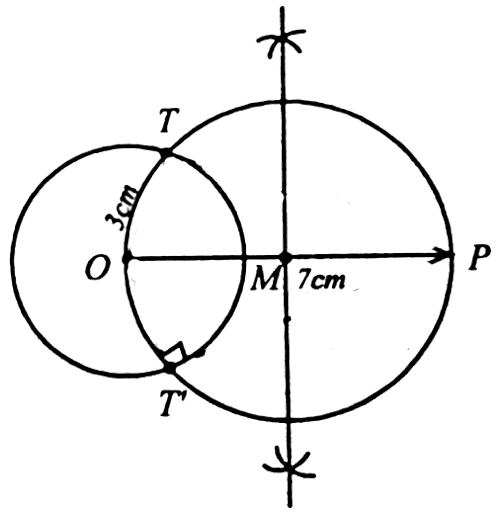
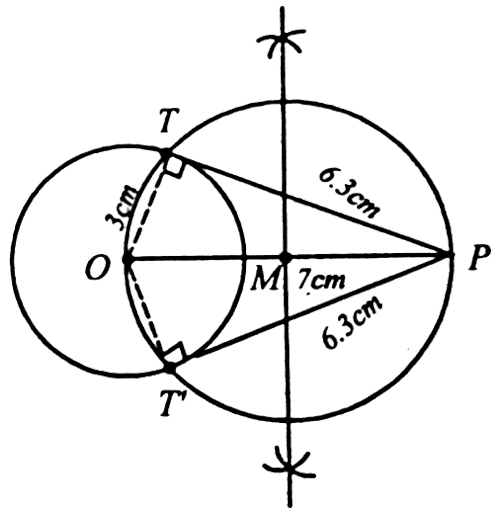
| 1) Draw a circe of radius 3cm. From an external point 7cm away from its centre, construct the pair of tangents to the circle and measure their lengths. SOLUTION 1 : (i) With O as the centre draw circle of radius 3cm. (ii) Mark a point P at a distance of 7cm from O and join OP.
(iii) Draw the perpendicuar bisector of OP. Let it meet OP at M. (iv) With M as centre and MO as radius, draw another circle.
(v) Let the two circles intersect at T and T’
(vi) Join PT and PT’. They are the required tangents.
Length of the tangent, PT = 6.3cm
|
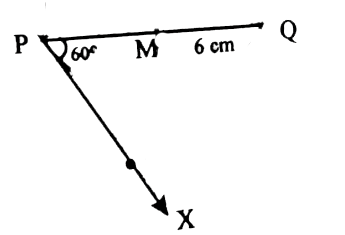
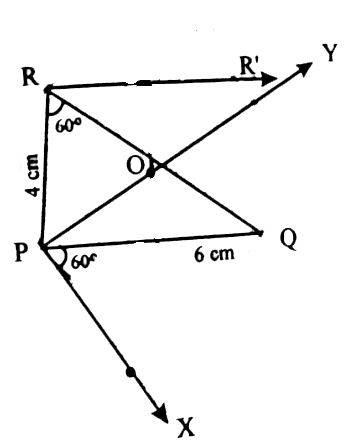
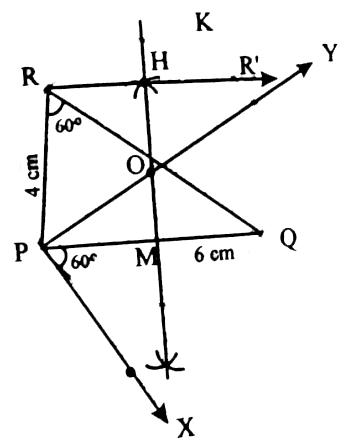
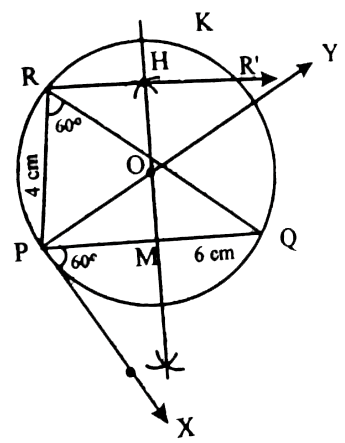
| 2) Construct a ►PQR in which the base PQ = 6cm, ∠R = 60 ° and the altitude from R to PQ is 4cm SOLUTION 1 : (i) Draw the line segment PQ = 6cm. (ii) Draw PX such that ∠QPX = 60 ° (iii) Draw the perpendicular bisectors of PQ intersecting PY at O and PQ at M. (iv) With O as center and OP as radius, draw the circle KPQ.
(v) The segment PKQ. (vi) Onthe perpendicular bisector MO, make the point H such that MH = 4cm.
(vii) Draw the RHS‛ parallel to PQ meeting the circle at R and R‛. (viii) complet the ►PQR, which is one of thenrequired triangles.
|
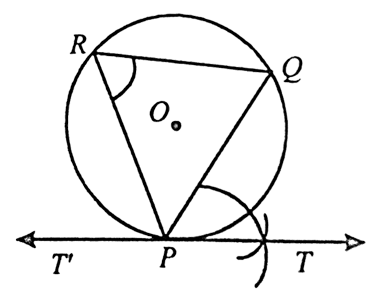
| 3) Draw a circle of radius 3.2cm. At a point P on it, draw a tangent to the circle using the tangent -chord therem.
SOLUTION 1 : Given : The radius of the circle = 3.2cm. Construction : (i) With O as the centre draw a circle of radius 3.2cm. (ii) Take a point P on the circle.
(ii) Thourth P, draw any chord PQ. (iv) mark a R distinct from P and Q on the circle so that P,Q are in counter clockwise direction. (v) Join PR and QR.
(vi) At P, construst ∠ QPT = ∠PRQ. (vii) Product TP to T to get the required tangent line T PT.
|
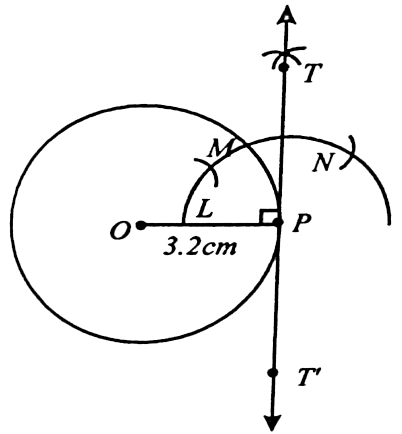
| 4) Draw a circle of radius 3.2cm. Take a point P on this circle and draw a tangent at P. (using the centre).
SOLUTION 1 : Given : radius of circle = 3.2cm Coustruction : With O as the centre draw a circle of radius 3.2cm.
(ii) Take a point P on the circle and join OP. (iii) Draw an arc of a circle with centre at P cutting OP at L.
(iv) Mark M and N on the arc such that LM = MN
(vi) T P to T to get the required tangent T PT.
|
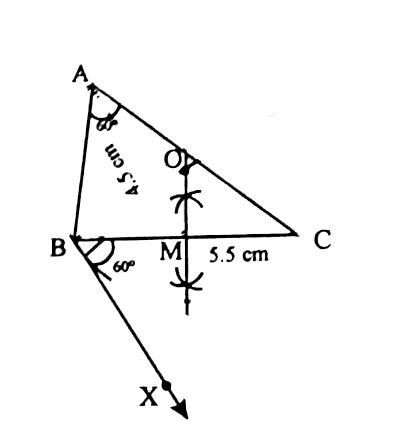
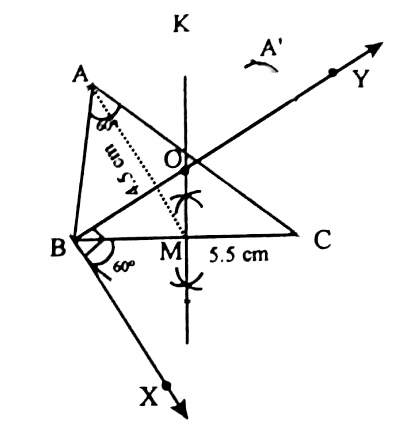
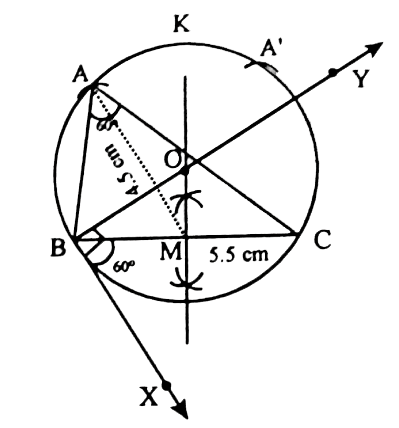
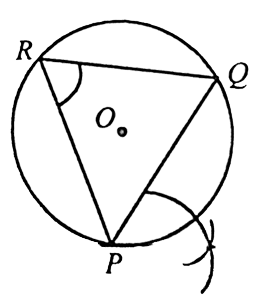
| 5) Construct a ► ABC in which BC =5.5cm.<A = 60 °. And the median AM from vertex aA is 4.5cm. SOLUTION 1 : (i) Draw a line segment BC =5.5cm. (ii) Though B draw BX such that <CBX = 60 °
(iii)Draw the perpendicuar bisector of BC intersectiong BY at O and BC at M.
(iv) Draw BY perpendicuar to BX. (v)With O as centre and OB as radius,draw the circle.
(vi)The major arc BKC of the circle, contains the vertical angle 60 °
|
| 6) Draw a circe of radius 3cm. From an external point 7cm away from its centre, construct the pair of tangents to the circle and measure their lengths. SOLUTION 1 : (i) With O as the centre draw circle of radius 3cm. (ii) Mark a point P at a distance of 7cm from O and join OP.
(iii) Draw the perpendicuar bisector of OP. Let it meet OP at M. (iv) With M as centre and MO as radius, draw another circle.
(v) Let the two circles intersect at T and T’
(vi) Join PT and PT’. They are the required tangents.
Length of the tangent, PT = 6.3cm
|
| 7) Construct a ►PQR in which the base PQ = 6cm, ∠R = 60 ° and the altitude from R to PQ is 4cm SOLUTION 1 : (i) Draw the line segment PQ = 6cm. (ii) Draw PX such that ∠QPX = 60 ° (iii) Draw the perpendicular bisectors of PQ intersecting PY at O and PQ at M. (iv) With O as center and OP as radius, draw the circle KPQ.
(v) The segment PKQ. (vi) Onthe perpendicular bisector MO, make the point H such that MH = 4cm.
(vii) Draw the RHS‛ parallel to PQ meeting the circle at R and R‛. (viii) complet the ►PQR, which is one of thenrequired triangles.
|
| 8) Draw a circle of radius 3.2cm. At a point P on it, draw a tangent to the circle using the tangent -chord therem.
SOLUTION 1 : Given : The radius of the circle = 3.2cm. Construction : (i) With O as the centre draw a circle of radius 3.2cm. (ii) Take a point P on the circle.
(ii) Thourth P, draw any chord PQ. (iv) mark a R distinct from P and Q on the circle so that P,Q are in counter clockwise direction. (v) Join PR and QR.
(vi) At P, construst ∠ QPT = ∠PRQ. (vii) Product TP to T to get the required tangent line T PT.
|
| 9) Draw a circle of radius 3.2cm. Take a point P on this circle and draw a tangent at P. (using the centre).
SOLUTION 1 : Given : radius of circle = 3.2cm Coustruction : With O as the centre draw a circle of radius 3.2cm.
(ii) Take a point P on the circle and join OP. (iii) Draw an arc of a circle with centre at P cutting OP at L.
(iv) Mark M and N on the arc such that LM = MN
(vi) T P to T to get the required tangent T PT.
|
| 10) Construct a ► ABC in which BC =5.5cm.<A = 60 °. And the median AM from vertex aA is 4.5cm. SOLUTION 1 : (i) Draw a line segment BC =5.5cm. (ii) Though B draw BX such that <CBX = 60 °
(iii)Draw the perpendicuar bisector of BC intersectiong BY at O and BC at M.
(iv) Draw BY perpendicuar to BX. (v)With O as centre and OB as radius,draw the circle.
(vi)The major arc BKC of the circle, contains the vertical angle 60 °
|

.png)