Scroll:Theorem: >> Theorem >> saq (4155)

Written Instructions:

For each Multiple Choice Question (MCQ), four options are given. One of them is the correct answer. Make your choice (1,2,3 or 4). Write your answers in the brackets provided..

For each Short Answer Question(SAQ) and Long Answer Question(LAQ), write your answers in the blanks provided.

Leave your answers in the simplest form or correct to two decimal places.


 

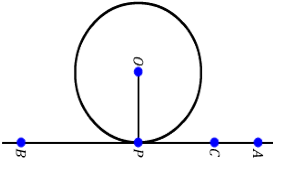
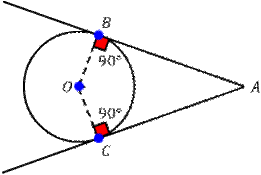
1)  

1. Summary
A straight line intersects a circle at one or two point. The tangent to a circle is a line that touches the circle at one point. Secant intersects the circle at two points.

Point of contact:
The point at which the straight line touches the circle is called the point of contact or point of tangency.

Some properties of tangents to a circle:

Infinite number of tangents can be drawn to a circle but only one tangent can be drawn at any given point on a circle.
From an external point to can draw two tangents of equal length.
The radius of the circle is perpendicular to the tangent at its point of contact and the tangents drawn at the extremities of the diameter of a circle are parallel.



radius perpendicular to tangent, radius and tangent, diameter and tangent tangents from external point, external point, tangents to a circle, tangents, tangents of equal length, equality of two tangents, tangents from outside the circle, tangents from outside

Theorem:
The tangent at any point on a circle is perpendicular to the radius drawn to the point of contact.


Given: A tangent AB with point of contact P.
To prove: OP ⊥ AB
Proof:
Consider point C on AB other than P.
C must lie outside the circle. (∵ A tangent can have only one point of contact with the circle)
OC > OP (∵ C lies outside the circle)
This is true for all positions of C on AB.
Thus, OP is the shortest distance between point P and line segment AB.
Hence, OP ⊥ AB.

Theorem:
Tangents drawn to a circle from an external point are equal in length.

 

Given: Two tangents AB and AC from an external point A to points B and C on a circle.
To prove: AB = AC
Construction: Join OA, OB and OC.
Proof:
In triangles OAB and OAC,
∠OBA = 90o (Radius OB ⊥ Tangent AB at B)
∠OCA = 90o (Radius OC ⊥ Tangent AC at C)
In triangles OBA and OCA,
∠OBA = ∠OCA = 90o
OB = OC (Radii of the same circle)
OA = OA (Common side)
Thus, ΔOBA ≅ ΔOCA (RHS congruence rule)
Hence, AB = AC (Corresponding sides of congruent triangles)
The tangents drawn at the extremities of the diameter of a circle are parallel.



Answer:_______________




2)  

1. Summary
A straight line intersects a circle at one or two point. The tangent to a circle is a line that touches the circle at one point. Secant intersects the circle at two points.

Point of contact:
The point at which the straight line touches the circle is called the point of contact or point of tangency.

Some properties of tangents to a circle:

Infinite number of tangents can be drawn to a circle but only one tangent can be drawn at any given point on a circle.
From an external point to can draw two tangents of equal length.
The radius of the circle is perpendicular to the tangent at its point of contact and the tangents drawn at the extremities of the diameter of a circle are parallel.



radius perpendicular to tangent, radius and tangent, diameter and tangent tangents from external point, external point, tangents to a circle, tangents, tangents of equal length, equality of two tangents, tangents from outside the circle, tangents from outside

Theorem:
The tangent at any point on a circle is perpendicular to the radius drawn to the point of contact.


Given: A tangent AB with point of contact P.
To prove: OP ⊥ AB
Proof:
Consider point C on AB other than P.
C must lie outside the circle. (∵ A tangent can have only one point of contact with the circle)
OC > OP (∵ C lies outside the circle)
This is true for all positions of C on AB.
Thus, OP is the shortest distance between point P and line segment AB.
Hence, OP ⊥ AB.

Theorem:
Tangents drawn to a circle from an external point are equal in length.

 

Given: Two tangents AB and AC from an external point A to points B and C on a circle.
To prove: AB = AC
Construction: Join OA, OB and OC.
Proof:
In triangles OAB and OAC,
∠OBA = 90o (Radius OB ⊥ Tangent AB at B)
∠OCA = 90o (Radius OC ⊥ Tangent AC at C)
In triangles OBA and OCA,
∠OBA = ∠OCA = 90o
OB = OC (Radii of the same circle)
OA = OA (Common side)
Thus, ΔOBA ≅ ΔOCA (RHS congruence rule)
Hence, AB = AC (Corresponding sides of congruent triangles)
The tangents drawn at the extremities of the diameter of a circle are parallel.



Answer:_______________




3)  

1. Summary
A straight line intersects a circle at one or two point. The tangent to a circle is a line that touches the circle at one point. Secant intersects the circle at two points.

Point of contact:
The point at which the straight line touches the circle is called the point of contact or point of tangency.

Some properties of tangents to a circle:

Infinite number of tangents can be drawn to a circle but only one tangent can be drawn at any given point on a circle.
From an external point to can draw two tangents of equal length.
The radius of the circle is perpendicular to the tangent at its point of contact and the tangents drawn at the extremities of the diameter of a circle are parallel.



radius perpendicular to tangent, radius and tangent, diameter and tangent tangents from external point, external point, tangents to a circle, tangents, tangents of equal length, equality of two tangents, tangents from outside the circle, tangents from outside

Theorem:
The tangent at any point on a circle is perpendicular to the radius drawn to the point of contact.


Given: A tangent AB with point of contact P.
To prove: OP ⊥ AB
Proof:
Consider point C on AB other than P.
C must lie outside the circle. (∵ A tangent can have only one point of contact with the circle)
OC > OP (∵ C lies outside the circle)
This is true for all positions of C on AB.
Thus, OP is the shortest distance between point P and line segment AB.
Hence, OP ⊥ AB.

Theorem:
Tangents drawn to a circle from an external point are equal in length.

 

Given: Two tangents AB and AC from an external point A to points B and C on a circle.
To prove: AB = AC
Construction: Join OA, OB and OC.
Proof:
In triangles OAB and OAC,
∠OBA = 90o (Radius OB ⊥ Tangent AB at B)
∠OCA = 90o (Radius OC ⊥ Tangent AC at C)
In triangles OBA and OCA,
∠OBA = ∠OCA = 90o
OB = OC (Radii of the same circle)
OA = OA (Common side)
Thus, ΔOBA ≅ ΔOCA (RHS congruence rule)
Hence, AB = AC (Corresponding sides of congruent triangles)
The tangents drawn at the extremities of the diameter of a circle are parallel.



Answer:_______________




4)  

1. Summary
A straight line intersects a circle at one or two point. The tangent to a circle is a line that touches the circle at one point. Secant intersects the circle at two points.

Point of contact:
The point at which the straight line touches the circle is called the point of contact or point of tangency.

Some properties of tangents to a circle:

Infinite number of tangents can be drawn to a circle but only one tangent can be drawn at any given point on a circle.
From an external point to can draw two tangents of equal length.
The radius of the circle is perpendicular to the tangent at its point of contact and the tangents drawn at the extremities of the diameter of a circle are parallel.



radius perpendicular to tangent, radius and tangent, diameter and tangent tangents from external point, external point, tangents to a circle, tangents, tangents of equal length, equality of two tangents, tangents from outside the circle, tangents from outside

Theorem:
The tangent at any point on a circle is perpendicular to the radius drawn to the point of contact.


Given: A tangent AB with point of contact P.
To prove: OP ⊥ AB
Proof:
Consider point C on AB other than P.
C must lie outside the circle. (∵ A tangent can have only one point of contact with the circle)
OC > OP (∵ C lies outside the circle)
This is true for all positions of C on AB.
Thus, OP is the shortest distance between point P and line segment AB.
Hence, OP ⊥ AB.

Theorem:
Tangents drawn to a circle from an external point are equal in length.

 

Given: Two tangents AB and AC from an external point A to points B and C on a circle.
To prove: AB = AC
Construction: Join OA, OB and OC.
Proof:
In triangles OAB and OAC,
∠OBA = 90o (Radius OB ⊥ Tangent AB at B)
∠OCA = 90o (Radius OC ⊥ Tangent AC at C)
In triangles OBA and OCA,
∠OBA = ∠OCA = 90o
OB = OC (Radii of the same circle)
OA = OA (Common side)
Thus, ΔOBA ≅ ΔOCA (RHS congruence rule)
Hence, AB = AC (Corresponding sides of congruent triangles)
The tangents drawn at the extremities of the diameter of a circle are parallel.



Answer:_______________




5)  

1. Summary
A straight line intersects a circle at one or two point. The tangent to a circle is a line that touches the circle at one point. Secant intersects the circle at two points.

Point of contact:
The point at which the straight line touches the circle is called the point of contact or point of tangency.

Some properties of tangents to a circle:

Infinite number of tangents can be drawn to a circle but only one tangent can be drawn at any given point on a circle.
From an external point to can draw two tangents of equal length.
The radius of the circle is perpendicular to the tangent at its point of contact and the tangents drawn at the extremities of the diameter of a circle are parallel.



radius perpendicular to tangent, radius and tangent, diameter and tangent tangents from external point, external point, tangents to a circle, tangents, tangents of equal length, equality of two tangents, tangents from outside the circle, tangents from outside

Theorem:
The tangent at any point on a circle is perpendicular to the radius drawn to the point of contact.


Given: A tangent AB with point of contact P.
To prove: OP ⊥ AB
Proof:
Consider point C on AB other than P.
C must lie outside the circle. (∵ A tangent can have only one point of contact with the circle)
OC > OP (∵ C lies outside the circle)
This is true for all positions of C on AB.
Thus, OP is the shortest distance between point P and line segment AB.
Hence, OP ⊥ AB.

Theorem:
Tangents drawn to a circle from an external point are equal in length.

 

Given: Two tangents AB and AC from an external point A to points B and C on a circle.
To prove: AB = AC
Construction: Join OA, OB and OC.
Proof:
In triangles OAB and OAC,
∠OBA = 90o (Radius OB ⊥ Tangent AB at B)
∠OCA = 90o (Radius OC ⊥ Tangent AC at C)
In triangles OBA and OCA,
∠OBA = ∠OCA = 90o
OB = OC (Radii of the same circle)
OA = OA (Common side)
Thus, ΔOBA ≅ ΔOCA (RHS congruence rule)
Hence, AB = AC (Corresponding sides of congruent triangles)
The tangents drawn at the extremities of the diameter of a circle are parallel.



Answer:_______________




6)  

1. Summary
A straight line intersects a circle at one or two point. The tangent to a circle is a line that touches the circle at one point. Secant intersects the circle at two points.

Point of contact:
The point at which the straight line touches the circle is called the point of contact or point of tangency.

Some properties of tangents to a circle:

Infinite number of tangents can be drawn to a circle but only one tangent can be drawn at any given point on a circle.
From an external point to can draw two tangents of equal length.
The radius of the circle is perpendicular to the tangent at its point of contact and the tangents drawn at the extremities of the diameter of a circle are parallel.



radius perpendicular to tangent, radius and tangent, diameter and tangent tangents from external point, external point, tangents to a circle, tangents, tangents of equal length, equality of two tangents, tangents from outside the circle, tangents from outside

Theorem:
The tangent at any point on a circle is perpendicular to the radius drawn to the point of contact.


Given: A tangent AB with point of contact P.
To prove: OP ⊥ AB
Proof:
Consider point C on AB other than P.
C must lie outside the circle. (∵ A tangent can have only one point of contact with the circle)
OC > OP (∵ C lies outside the circle)
This is true for all positions of C on AB.
Thus, OP is the shortest distance between point P and line segment AB.
Hence, OP ⊥ AB.

Theorem:
Tangents drawn to a circle from an external point are equal in length.

 

Given: Two tangents AB and AC from an external point A to points B and C on a circle.
To prove: AB = AC
Construction: Join OA, OB and OC.
Proof:
In triangles OAB and OAC,
∠OBA = 90o (Radius OB ⊥ Tangent AB at B)
∠OCA = 90o (Radius OC ⊥ Tangent AC at C)
In triangles OBA and OCA,
∠OBA = ∠OCA = 90o
OB = OC (Radii of the same circle)
OA = OA (Common side)
Thus, ΔOBA ≅ ΔOCA (RHS congruence rule)
Hence, AB = AC (Corresponding sides of congruent triangles)
The tangents drawn at the extremities of the diameter of a circle are parallel.



Answer:_______________




7)  

1. Summary
A straight line intersects a circle at one or two point. The tangent to a circle is a line that touches the circle at one point. Secant intersects the circle at two points.

Point of contact:
The point at which the straight line touches the circle is called the point of contact or point of tangency.

Some properties of tangents to a circle:

Infinite number of tangents can be drawn to a circle but only one tangent can be drawn at any given point on a circle.
From an external point to can draw two tangents of equal length.
The radius of the circle is perpendicular to the tangent at its point of contact and the tangents drawn at the extremities of the diameter of a circle are parallel.



radius perpendicular to tangent, radius and tangent, diameter and tangent tangents from external point, external point, tangents to a circle, tangents, tangents of equal length, equality of two tangents, tangents from outside the circle, tangents from outside

Theorem:
The tangent at any point on a circle is perpendicular to the radius drawn to the point of contact.


Given: A tangent AB with point of contact P.
To prove: OP ⊥ AB
Proof:
Consider point C on AB other than P.
C must lie outside the circle. (∵ A tangent can have only one point of contact with the circle)
OC > OP (∵ C lies outside the circle)
This is true for all positions of C on AB.
Thus, OP is the shortest distance between point P and line segment AB.
Hence, OP ⊥ AB.

Theorem:
Tangents drawn to a circle from an external point are equal in length.

 

Given: Two tangents AB and AC from an external point A to points B and C on a circle.
To prove: AB = AC
Construction: Join OA, OB and OC.
Proof:
In triangles OAB and OAC,
∠OBA = 90o (Radius OB ⊥ Tangent AB at B)
∠OCA = 90o (Radius OC ⊥ Tangent AC at C)
In triangles OBA and OCA,
∠OBA = ∠OCA = 90o
OB = OC (Radii of the same circle)
OA = OA (Common side)
Thus, ΔOBA ≅ ΔOCA (RHS congruence rule)
Hence, AB = AC (Corresponding sides of congruent triangles)
The tangents drawn at the extremities of the diameter of a circle are parallel.



Answer:_______________




8)  

1. Summary
A straight line intersects a circle at one or two point. The tangent to a circle is a line that touches the circle at one point. Secant intersects the circle at two points.

Point of contact:
The point at which the straight line touches the circle is called the point of contact or point of tangency.

Some properties of tangents to a circle:

Infinite number of tangents can be drawn to a circle but only one tangent can be drawn at any given point on a circle.
From an external point to can draw two tangents of equal length.
The radius of the circle is perpendicular to the tangent at its point of contact and the tangents drawn at the extremities of the diameter of a circle are parallel.



radius perpendicular to tangent, radius and tangent, diameter and tangent tangents from external point, external point, tangents to a circle, tangents, tangents of equal length, equality of two tangents, tangents from outside the circle, tangents from outside

Theorem:
The tangent at any point on a circle is perpendicular to the radius drawn to the point of contact.


Given: A tangent AB with point of contact P.
To prove: OP ⊥ AB
Proof:
Consider point C on AB other than P.
C must lie outside the circle. (∵ A tangent can have only one point of contact with the circle)
OC > OP (∵ C lies outside the circle)
This is true for all positions of C on AB.
Thus, OP is the shortest distance between point P and line segment AB.
Hence, OP ⊥ AB.

Theorem:
Tangents drawn to a circle from an external point are equal in length.

 

Given: Two tangents AB and AC from an external point A to points B and C on a circle.
To prove: AB = AC
Construction: Join OA, OB and OC.
Proof:
In triangles OAB and OAC,
∠OBA = 90o (Radius OB ⊥ Tangent AB at B)
∠OCA = 90o (Radius OC ⊥ Tangent AC at C)
In triangles OBA and OCA,
∠OBA = ∠OCA = 90o
OB = OC (Radii of the same circle)
OA = OA (Common side)
Thus, ΔOBA ≅ ΔOCA (RHS congruence rule)
Hence, AB = AC (Corresponding sides of congruent triangles)
The tangents drawn at the extremities of the diameter of a circle are parallel.



Answer:_______________




9)  

1. Summary
A straight line intersects a circle at one or two point. The tangent to a circle is a line that touches the circle at one point. Secant intersects the circle at two points.

Point of contact:
The point at which the straight line touches the circle is called the point of contact or point of tangency.

Some properties of tangents to a circle:

Infinite number of tangents can be drawn to a circle but only one tangent can be drawn at any given point on a circle.
From an external point to can draw two tangents of equal length.
The radius of the circle is perpendicular to the tangent at its point of contact and the tangents drawn at the extremities of the diameter of a circle are parallel.



radius perpendicular to tangent, radius and tangent, diameter and tangent tangents from external point, external point, tangents to a circle, tangents, tangents of equal length, equality of two tangents, tangents from outside the circle, tangents from outside

Theorem:
The tangent at any point on a circle is perpendicular to the radius drawn to the point of contact.


Given: A tangent AB with point of contact P.
To prove: OP ⊥ AB
Proof:
Consider point C on AB other than P.
C must lie outside the circle. (∵ A tangent can have only one point of contact with the circle)
OC > OP (∵ C lies outside the circle)
This is true for all positions of C on AB.
Thus, OP is the shortest distance between point P and line segment AB.
Hence, OP ⊥ AB.

Theorem:
Tangents drawn to a circle from an external point are equal in length.

 

Given: Two tangents AB and AC from an external point A to points B and C on a circle.
To prove: AB = AC
Construction: Join OA, OB and OC.
Proof:
In triangles OAB and OAC,
∠OBA = 90o (Radius OB ⊥ Tangent AB at B)
∠OCA = 90o (Radius OC ⊥ Tangent AC at C)
In triangles OBA and OCA,
∠OBA = ∠OCA = 90o
OB = OC (Radii of the same circle)
OA = OA (Common side)
Thus, ΔOBA ≅ ΔOCA (RHS congruence rule)
Hence, AB = AC (Corresponding sides of congruent triangles)
The tangents drawn at the extremities of the diameter of a circle are parallel.



Answer:_______________




10)  

1. Summary
A straight line intersects a circle at one or two point. The tangent to a circle is a line that touches the circle at one point. Secant intersects the circle at two points.

Point of contact:
The point at which the straight line touches the circle is called the point of contact or point of tangency.

Some properties of tangents to a circle:

Infinite number of tangents can be drawn to a circle but only one tangent can be drawn at any given point on a circle.
From an external point to can draw two tangents of equal length.
The radius of the circle is perpendicular to the tangent at its point of contact and the tangents drawn at the extremities of the diameter of a circle are parallel.



radius perpendicular to tangent, radius and tangent, diameter and tangent tangents from external point, external point, tangents to a circle, tangents, tangents of equal length, equality of two tangents, tangents from outside the circle, tangents from outside

Theorem:
The tangent at any point on a circle is perpendicular to the radius drawn to the point of contact.


Given: A tangent AB with point of contact P.
To prove: OP ⊥ AB
Proof:
Consider point C on AB other than P.
C must lie outside the circle. (∵ A tangent can have only one point of contact with the circle)
OC > OP (∵ C lies outside the circle)
This is true for all positions of C on AB.
Thus, OP is the shortest distance between point P and line segment AB.
Hence, OP ⊥ AB.

Theorem:
Tangents drawn to a circle from an external point are equal in length.

 

Given: Two tangents AB and AC from an external point A to points B and C on a circle.
To prove: AB = AC
Construction: Join OA, OB and OC.
Proof:
In triangles OAB and OAC,
∠OBA = 90o (Radius OB ⊥ Tangent AB at B)
∠OCA = 90o (Radius OC ⊥ Tangent AC at C)
In triangles OBA and OCA,
∠OBA = ∠OCA = 90o
OB = OC (Radii of the same circle)
OA = OA (Common side)
Thus, ΔOBA ≅ ΔOCA (RHS congruence rule)
Hence, AB = AC (Corresponding sides of congruent triangles)
The tangents drawn at the extremities of the diameter of a circle are parallel.



Answer:_______________




 

1)  

1. Summary
A straight line intersects a circle at one or two point. The tangent to a circle is a line that touches the circle at one point. Secant intersects the circle at two points.

Point of contact:
The point at which the straight line touches the circle is called the point of contact or point of tangency.

Some properties of tangents to a circle:

Infinite number of tangents can be drawn to a circle but only one tangent can be drawn at any given point on a circle.
From an external point to can draw two tangents of equal length.
The radius of the circle is perpendicular to the tangent at its point of contact and the tangents drawn at the extremities of the diameter of a circle are parallel.



radius perpendicular to tangent, radius and tangent, diameter and tangent tangents from external point, external point, tangents to a circle, tangents, tangents of equal length, equality of two tangents, tangents from outside the circle, tangents from outside

Theorem:
The tangent at any point on a circle is perpendicular to the radius drawn to the point of contact.


Given: A tangent AB with point of contact P.
To prove: OP ⊥ AB
Proof:
Consider point C on AB other than P.
C must lie outside the circle. (∵ A tangent can have only one point of contact with the circle)
OC > OP (∵ C lies outside the circle)
This is true for all positions of C on AB.
Thus, OP is the shortest distance between point P and line segment AB.
Hence, OP ⊥ AB.

Theorem:
Tangents drawn to a circle from an external point are equal in length.

 

Given: Two tangents AB and AC from an external point A to points B and C on a circle.
To prove: AB = AC
Construction: Join OA, OB and OC.
Proof:
In triangles OAB and OAC,
∠OBA = 90o (Radius OB ⊥ Tangent AB at B)
∠OCA = 90o (Radius OC ⊥ Tangent AC at C)
In triangles OBA and OCA,
∠OBA = ∠OCA = 90o
OB = OC (Radii of the same circle)
OA = OA (Common side)
Thus, ΔOBA ≅ ΔOCA (RHS congruence rule)
Hence, AB = AC (Corresponding sides of congruent triangles)
The tangents drawn at the extremities of the diameter of a circle are parallel.




2)  

1. Summary
A straight line intersects a circle at one or two point. The tangent to a circle is a line that touches the circle at one point. Secant intersects the circle at two points.

Point of contact:
The point at which the straight line touches the circle is called the point of contact or point of tangency.

Some properties of tangents to a circle:

Infinite number of tangents can be drawn to a circle but only one tangent can be drawn at any given point on a circle.
From an external point to can draw two tangents of equal length.
The radius of the circle is perpendicular to the tangent at its point of contact and the tangents drawn at the extremities of the diameter of a circle are parallel.



radius perpendicular to tangent, radius and tangent, diameter and tangent tangents from external point, external point, tangents to a circle, tangents, tangents of equal length, equality of two tangents, tangents from outside the circle, tangents from outside

Theorem:
The tangent at any point on a circle is perpendicular to the radius drawn to the point of contact.


Given: A tangent AB with point of contact P.
To prove: OP ⊥ AB
Proof:
Consider point C on AB other than P.
C must lie outside the circle. (∵ A tangent can have only one point of contact with the circle)
OC > OP (∵ C lies outside the circle)
This is true for all positions of C on AB.
Thus, OP is the shortest distance between point P and line segment AB.
Hence, OP ⊥ AB.

Theorem:
Tangents drawn to a circle from an external point are equal in length.

 

Given: Two tangents AB and AC from an external point A to points B and C on a circle.
To prove: AB = AC
Construction: Join OA, OB and OC.
Proof:
In triangles OAB and OAC,
∠OBA = 90o (Radius OB ⊥ Tangent AB at B)
∠OCA = 90o (Radius OC ⊥ Tangent AC at C)
In triangles OBA and OCA,
∠OBA = ∠OCA = 90o
OB = OC (Radii of the same circle)
OA = OA (Common side)
Thus, ΔOBA ≅ ΔOCA (RHS congruence rule)
Hence, AB = AC (Corresponding sides of congruent triangles)
The tangents drawn at the extremities of the diameter of a circle are parallel.




3)  

1. Summary
A straight line intersects a circle at one or two point. The tangent to a circle is a line that touches the circle at one point. Secant intersects the circle at two points.

Point of contact:
The point at which the straight line touches the circle is called the point of contact or point of tangency.

Some properties of tangents to a circle:

Infinite number of tangents can be drawn to a circle but only one tangent can be drawn at any given point on a circle.
From an external point to can draw two tangents of equal length.
The radius of the circle is perpendicular to the tangent at its point of contact and the tangents drawn at the extremities of the diameter of a circle are parallel.



radius perpendicular to tangent, radius and tangent, diameter and tangent tangents from external point, external point, tangents to a circle, tangents, tangents of equal length, equality of two tangents, tangents from outside the circle, tangents from outside

Theorem:
The tangent at any point on a circle is perpendicular to the radius drawn to the point of contact.


Given: A tangent AB with point of contact P.
To prove: OP ⊥ AB
Proof:
Consider point C on AB other than P.
C must lie outside the circle. (∵ A tangent can have only one point of contact with the circle)
OC > OP (∵ C lies outside the circle)
This is true for all positions of C on AB.
Thus, OP is the shortest distance between point P and line segment AB.
Hence, OP ⊥ AB.

Theorem:
Tangents drawn to a circle from an external point are equal in length.

 

Given: Two tangents AB and AC from an external point A to points B and C on a circle.
To prove: AB = AC
Construction: Join OA, OB and OC.
Proof:
In triangles OAB and OAC,
∠OBA = 90o (Radius OB ⊥ Tangent AB at B)
∠OCA = 90o (Radius OC ⊥ Tangent AC at C)
In triangles OBA and OCA,
∠OBA = ∠OCA = 90o
OB = OC (Radii of the same circle)
OA = OA (Common side)
Thus, ΔOBA ≅ ΔOCA (RHS congruence rule)
Hence, AB = AC (Corresponding sides of congruent triangles)
The tangents drawn at the extremities of the diameter of a circle are parallel.




4)  

1. Summary
A straight line intersects a circle at one or two point. The tangent to a circle is a line that touches the circle at one point. Secant intersects the circle at two points.

Point of contact:
The point at which the straight line touches the circle is called the point of contact or point of tangency.

Some properties of tangents to a circle:

Infinite number of tangents can be drawn to a circle but only one tangent can be drawn at any given point on a circle.
From an external point to can draw two tangents of equal length.
The radius of the circle is perpendicular to the tangent at its point of contact and the tangents drawn at the extremities of the diameter of a circle are parallel.



radius perpendicular to tangent, radius and tangent, diameter and tangent tangents from external point, external point, tangents to a circle, tangents, tangents of equal length, equality of two tangents, tangents from outside the circle, tangents from outside

Theorem:
The tangent at any point on a circle is perpendicular to the radius drawn to the point of contact.


Given: A tangent AB with point of contact P.
To prove: OP ⊥ AB
Proof:
Consider point C on AB other than P.
C must lie outside the circle. (∵ A tangent can have only one point of contact with the circle)
OC > OP (∵ C lies outside the circle)
This is true for all positions of C on AB.
Thus, OP is the shortest distance between point P and line segment AB.
Hence, OP ⊥ AB.

Theorem:
Tangents drawn to a circle from an external point are equal in length.

 

Given: Two tangents AB and AC from an external point A to points B and C on a circle.
To prove: AB = AC
Construction: Join OA, OB and OC.
Proof:
In triangles OAB and OAC,
∠OBA = 90o (Radius OB ⊥ Tangent AB at B)
∠OCA = 90o (Radius OC ⊥ Tangent AC at C)
In triangles OBA and OCA,
∠OBA = ∠OCA = 90o
OB = OC (Radii of the same circle)
OA = OA (Common side)
Thus, ΔOBA ≅ ΔOCA (RHS congruence rule)
Hence, AB = AC (Corresponding sides of congruent triangles)
The tangents drawn at the extremities of the diameter of a circle are parallel.




5)  

1. Summary
A straight line intersects a circle at one or two point. The tangent to a circle is a line that touches the circle at one point. Secant intersects the circle at two points.

Point of contact:
The point at which the straight line touches the circle is called the point of contact or point of tangency.

Some properties of tangents to a circle:

Infinite number of tangents can be drawn to a circle but only one tangent can be drawn at any given point on a circle.
From an external point to can draw two tangents of equal length.
The radius of the circle is perpendicular to the tangent at its point of contact and the tangents drawn at the extremities of the diameter of a circle are parallel.



radius perpendicular to tangent, radius and tangent, diameter and tangent tangents from external point, external point, tangents to a circle, tangents, tangents of equal length, equality of two tangents, tangents from outside the circle, tangents from outside

Theorem:
The tangent at any point on a circle is perpendicular to the radius drawn to the point of contact.


Given: A tangent AB with point of contact P.
To prove: OP ⊥ AB
Proof:
Consider point C on AB other than P.
C must lie outside the circle. (∵ A tangent can have only one point of contact with the circle)
OC > OP (∵ C lies outside the circle)
This is true for all positions of C on AB.
Thus, OP is the shortest distance between point P and line segment AB.
Hence, OP ⊥ AB.

Theorem:
Tangents drawn to a circle from an external point are equal in length.

 

Given: Two tangents AB and AC from an external point A to points B and C on a circle.
To prove: AB = AC
Construction: Join OA, OB and OC.
Proof:
In triangles OAB and OAC,
∠OBA = 90o (Radius OB ⊥ Tangent AB at B)
∠OCA = 90o (Radius OC ⊥ Tangent AC at C)
In triangles OBA and OCA,
∠OBA = ∠OCA = 90o
OB = OC (Radii of the same circle)
OA = OA (Common side)
Thus, ΔOBA ≅ ΔOCA (RHS congruence rule)
Hence, AB = AC (Corresponding sides of congruent triangles)
The tangents drawn at the extremities of the diameter of a circle are parallel.




6)  

1. Summary
A straight line intersects a circle at one or two point. The tangent to a circle is a line that touches the circle at one point. Secant intersects the circle at two points.

Point of contact:
The point at which the straight line touches the circle is called the point of contact or point of tangency.

Some properties of tangents to a circle:

Infinite number of tangents can be drawn to a circle but only one tangent can be drawn at any given point on a circle.
From an external point to can draw two tangents of equal length.
The radius of the circle is perpendicular to the tangent at its point of contact and the tangents drawn at the extremities of the diameter of a circle are parallel.



radius perpendicular to tangent, radius and tangent, diameter and tangent tangents from external point, external point, tangents to a circle, tangents, tangents of equal length, equality of two tangents, tangents from outside the circle, tangents from outside

Theorem:
The tangent at any point on a circle is perpendicular to the radius drawn to the point of contact.


Given: A tangent AB with point of contact P.
To prove: OP ⊥ AB
Proof:
Consider point C on AB other than P.
C must lie outside the circle. (∵ A tangent can have only one point of contact with the circle)
OC > OP (∵ C lies outside the circle)
This is true for all positions of C on AB.
Thus, OP is the shortest distance between point P and line segment AB.
Hence, OP ⊥ AB.

Theorem:
Tangents drawn to a circle from an external point are equal in length.

 

Given: Two tangents AB and AC from an external point A to points B and C on a circle.
To prove: AB = AC
Construction: Join OA, OB and OC.
Proof:
In triangles OAB and OAC,
∠OBA = 90o (Radius OB ⊥ Tangent AB at B)
∠OCA = 90o (Radius OC ⊥ Tangent AC at C)
In triangles OBA and OCA,
∠OBA = ∠OCA = 90o
OB = OC (Radii of the same circle)
OA = OA (Common side)
Thus, ΔOBA ≅ ΔOCA (RHS congruence rule)
Hence, AB = AC (Corresponding sides of congruent triangles)
The tangents drawn at the extremities of the diameter of a circle are parallel.




7)  

1. Summary
A straight line intersects a circle at one or two point. The tangent to a circle is a line that touches the circle at one point. Secant intersects the circle at two points.

Point of contact:
The point at which the straight line touches the circle is called the point of contact or point of tangency.

Some properties of tangents to a circle:

Infinite number of tangents can be drawn to a circle but only one tangent can be drawn at any given point on a circle.
From an external point to can draw two tangents of equal length.
The radius of the circle is perpendicular to the tangent at its point of contact and the tangents drawn at the extremities of the diameter of a circle are parallel.



radius perpendicular to tangent, radius and tangent, diameter and tangent tangents from external point, external point, tangents to a circle, tangents, tangents of equal length, equality of two tangents, tangents from outside the circle, tangents from outside

Theorem:
The tangent at any point on a circle is perpendicular to the radius drawn to the point of contact.


Given: A tangent AB with point of contact P.
To prove: OP ⊥ AB
Proof:
Consider point C on AB other than P.
C must lie outside the circle. (∵ A tangent can have only one point of contact with the circle)
OC > OP (∵ C lies outside the circle)
This is true for all positions of C on AB.
Thus, OP is the shortest distance between point P and line segment AB.
Hence, OP ⊥ AB.

Theorem:
Tangents drawn to a circle from an external point are equal in length.

 

Given: Two tangents AB and AC from an external point A to points B and C on a circle.
To prove: AB = AC
Construction: Join OA, OB and OC.
Proof:
In triangles OAB and OAC,
∠OBA = 90o (Radius OB ⊥ Tangent AB at B)
∠OCA = 90o (Radius OC ⊥ Tangent AC at C)
In triangles OBA and OCA,
∠OBA = ∠OCA = 90o
OB = OC (Radii of the same circle)
OA = OA (Common side)
Thus, ΔOBA ≅ ΔOCA (RHS congruence rule)
Hence, AB = AC (Corresponding sides of congruent triangles)
The tangents drawn at the extremities of the diameter of a circle are parallel.




8)  

1. Summary
A straight line intersects a circle at one or two point. The tangent to a circle is a line that touches the circle at one point. Secant intersects the circle at two points.

Point of contact:
The point at which the straight line touches the circle is called the point of contact or point of tangency.

Some properties of tangents to a circle:

Infinite number of tangents can be drawn to a circle but only one tangent can be drawn at any given point on a circle.
From an external point to can draw two tangents of equal length.
The radius of the circle is perpendicular to the tangent at its point of contact and the tangents drawn at the extremities of the diameter of a circle are parallel.



radius perpendicular to tangent, radius and tangent, diameter and tangent tangents from external point, external point, tangents to a circle, tangents, tangents of equal length, equality of two tangents, tangents from outside the circle, tangents from outside

Theorem:
The tangent at any point on a circle is perpendicular to the radius drawn to the point of contact.


Given: A tangent AB with point of contact P.
To prove: OP ⊥ AB
Proof:
Consider point C on AB other than P.
C must lie outside the circle. (∵ A tangent can have only one point of contact with the circle)
OC > OP (∵ C lies outside the circle)
This is true for all positions of C on AB.
Thus, OP is the shortest distance between point P and line segment AB.
Hence, OP ⊥ AB.

Theorem:
Tangents drawn to a circle from an external point are equal in length.

 

Given: Two tangents AB and AC from an external point A to points B and C on a circle.
To prove: AB = AC
Construction: Join OA, OB and OC.
Proof:
In triangles OAB and OAC,
∠OBA = 90o (Radius OB ⊥ Tangent AB at B)
∠OCA = 90o (Radius OC ⊥ Tangent AC at C)
In triangles OBA and OCA,
∠OBA = ∠OCA = 90o
OB = OC (Radii of the same circle)
OA = OA (Common side)
Thus, ΔOBA ≅ ΔOCA (RHS congruence rule)
Hence, AB = AC (Corresponding sides of congruent triangles)
The tangents drawn at the extremities of the diameter of a circle are parallel.




9)  

1. Summary
A straight line intersects a circle at one or two point. The tangent to a circle is a line that touches the circle at one point. Secant intersects the circle at two points.

Point of contact:
The point at which the straight line touches the circle is called the point of contact or point of tangency.

Some properties of tangents to a circle:

Infinite number of tangents can be drawn to a circle but only one tangent can be drawn at any given point on a circle.
From an external point to can draw two tangents of equal length.
The radius of the circle is perpendicular to the tangent at its point of contact and the tangents drawn at the extremities of the diameter of a circle are parallel.



radius perpendicular to tangent, radius and tangent, diameter and tangent tangents from external point, external point, tangents to a circle, tangents, tangents of equal length, equality of two tangents, tangents from outside the circle, tangents from outside

Theorem:
The tangent at any point on a circle is perpendicular to the radius drawn to the point of contact.


Given: A tangent AB with point of contact P.
To prove: OP ⊥ AB
Proof:
Consider point C on AB other than P.
C must lie outside the circle. (∵ A tangent can have only one point of contact with the circle)
OC > OP (∵ C lies outside the circle)
This is true for all positions of C on AB.
Thus, OP is the shortest distance between point P and line segment AB.
Hence, OP ⊥ AB.

Theorem:
Tangents drawn to a circle from an external point are equal in length.

 

Given: Two tangents AB and AC from an external point A to points B and C on a circle.
To prove: AB = AC
Construction: Join OA, OB and OC.
Proof:
In triangles OAB and OAC,
∠OBA = 90o (Radius OB ⊥ Tangent AB at B)
∠OCA = 90o (Radius OC ⊥ Tangent AC at C)
In triangles OBA and OCA,
∠OBA = ∠OCA = 90o
OB = OC (Radii of the same circle)
OA = OA (Common side)
Thus, ΔOBA ≅ ΔOCA (RHS congruence rule)
Hence, AB = AC (Corresponding sides of congruent triangles)
The tangents drawn at the extremities of the diameter of a circle are parallel.




10)  

1. Summary
A straight line intersects a circle at one or two point. The tangent to a circle is a line that touches the circle at one point. Secant intersects the circle at two points.

Point of contact:
The point at which the straight line touches the circle is called the point of contact or point of tangency.

Some properties of tangents to a circle:

Infinite number of tangents can be drawn to a circle but only one tangent can be drawn at any given point on a circle.
From an external point to can draw two tangents of equal length.
The radius of the circle is perpendicular to the tangent at its point of contact and the tangents drawn at the extremities of the diameter of a circle are parallel.



radius perpendicular to tangent, radius and tangent, diameter and tangent tangents from external point, external point, tangents to a circle, tangents, tangents of equal length, equality of two tangents, tangents from outside the circle, tangents from outside

Theorem:
The tangent at any point on a circle is perpendicular to the radius drawn to the point of contact.


Given: A tangent AB with point of contact P.
To prove: OP ⊥ AB
Proof:
Consider point C on AB other than P.
C must lie outside the circle. (∵ A tangent can have only one point of contact with the circle)
OC > OP (∵ C lies outside the circle)
This is true for all positions of C on AB.
Thus, OP is the shortest distance between point P and line segment AB.
Hence, OP ⊥ AB.

Theorem:
Tangents drawn to a circle from an external point are equal in length.

 

Given: Two tangents AB and AC from an external point A to points B and C on a circle.
To prove: AB = AC
Construction: Join OA, OB and OC.
Proof:
In triangles OAB and OAC,
∠OBA = 90o (Radius OB ⊥ Tangent AB at B)
∠OCA = 90o (Radius OC ⊥ Tangent AC at C)
In triangles OBA and OCA,
∠OBA = ∠OCA = 90o
OB = OC (Radii of the same circle)
OA = OA (Common side)
Thus, ΔOBA ≅ ΔOCA (RHS congruence rule)
Hence, AB = AC (Corresponding sides of congruent triangles)
The tangents drawn at the extremities of the diameter of a circle are parallel.