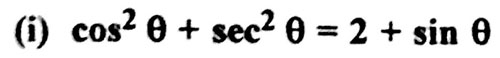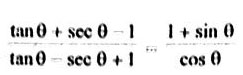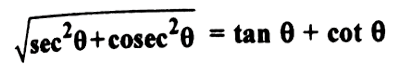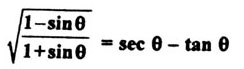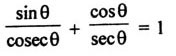Scroll:Trigonometry >> Prove the identity >> ps (4126)

Written Instructions:

For each Multiple Choice Question (MCQ), four options are given. One of them is the correct answer. Make your choice (1,2,3 or 4). Write your answers in the brackets provided..

For each Short Answer Question(SAQ) and Long Answer Question(LAQ), write your answers in the blanks provided.

Leave your answers in the simplest form or correct to two decimal places.


 

1)  

 Prove that, 

Ø

Ø

2Ø


Answer:_______________




2)  

 Determine whether each of the following is an identity or not.





Answer:_______________




3)  

 determine whether each of the following is an identity or not.




Answer:_______________




4)  

 If  x= a secØ + b tanØ and

     y= a tanØ + b secØ, then prove that x2 - y2 = a2 - b2




Answer:_______________




5)  

 Prove that  

Ø    

 Ø


Answer:_______________




6)  

Prove the following, 

Ø

Ø


Answer:_______________




7)  

 



 


Answer:_______________




8)  

prove that,  




Answer:_______________




9)  

 Prove the identity,



Answer:_______________




10)  

 Prove that, 

Ø

Ø

2Ø


Answer:_______________




 

1)  

 Prove that, 

Answer: 1-2secØ

Answer: tan Ø

Answer: 2tan2Ø



2)  

 Determine whether each of the following is an identity or not.



Answer: 1




3)  

 determine whether each of the following is an identity or not.



Answer: 2



4)  

 If  x= a secØ + b tanØ and

     y= a tanØ + b secØ, then prove that x2 - y2 = a2 - b2



Answer: 2


SOLUTION 1 :

 

      TO PROVE: x2 - y2 = a2 - b2

      PROOF:

              L.H.S. = x2 - y2

       =(a sec Ø + b tan Ø ) - (a tanØ + b secØ )2

       =[(a secØ ) + 2(a secØ ) (b tanØ ) + (b tanØ )2]

            - [(a tanØ )2 + 2 (a tanØ ) (b sinØ ) + (b sec Ø)2]

       = (a2 sec2Ø+ 2 ab secØ  tanØ + b2 tan2 Ø)

             -(a2 tan2Ø+ 2 ab tanØ  secØ  + b2  sec2Ø)

       = ( a2 sec2 Ø+ 2 ab secØ  tanØ + b2 tan2Ø)

            - (a2 tan2 Ø - 2 ab tanØ secØ + b2 sec2Ø) 

       = a2 sec2Ø- a2 tan2 Ø _ b2 tan2Ø- b2 sec2Ø

 

       = a2 (sec2Ø  - tan2Ø) - b2  (sec2 Ø- tan2Ø)

 

       =a2 (1) - b2 (1)

      =a2 - b2 = RHS 

           so R.H.S = L.H.S         Hence proved.



5)  

 Prove that  

Answer: 1+sinØ    

 Answer: cosØ



6)  

Prove the following, 

Answer: tanØ

Answer: cotØ



7)  

 



Answer: 1

 



8)  

prove that,  



Answer: 2



9)  

 Prove the identity,

Answer: 1



10)  

 Prove that, 

Answer: 1-2secØ

Answer: tan Ø

Answer: 2tan2Ø