Scroll:Measurement >> Area & Perimeter of Composite Figure >> ps (2904)
Written Instructions:
For each Multiple Choice Question (MCQ), four options are given. One of them is the correct answer. Make your choice (1,2,3 or 4). Write your answers in the brackets provided..
For each Short Answer Question(SAQ) and Long Answer Question(LAQ), write your answers in the blanks provided.
Leave your answers in the simplest form or correct to two decimal places.
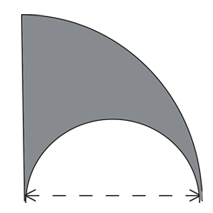
| 1) The figure below is formed by using a semi-circle and a quadrant. Find the perimeter and area of the shaded part, rounding your answers to the nearest whole number. π = 3.142
cm cm2 Answer:_______________ |
| 2) The figure below is formed by using a semi-circle and a quadrant. Find the perimeter and area of the shaded part, rounding your answers to the nearest whole number. π = 3.142
cm cm2 Answer:_______________ |
| 3) The figure below is formed by using a semi-circle and a quadrant. Find the perimeter and area of the shaded part, rounding your answers to the nearest whole number. π = 3.142
cm cm2 Answer:_______________ |
| 4) The figure below is formed by using a semi-circle and a quadrant. Find the perimeter and area of the shaded part, rounding your answers to the nearest whole number. π = 3.142
cm cm2 Answer:_______________ |
| 5) The figure below is formed by using a semi-circle and a quadrant. Find the perimeter and area of the shaded part, rounding your answers to the nearest whole number. π = 3.142
cm cm2 Answer:_______________ |
| 6) The figure below is formed by using a semi-circle and a quadrant. Find the perimeter and area of the shaded part, rounding your answers to the nearest whole number. π = 3.142
cm cm2 Answer:_______________ |
| 7) The figure below is formed by using a semi-circle and a quadrant. Find the perimeter and area of the shaded part, rounding your answers to the nearest whole number. π = 3.142
cm cm2 Answer:_______________ |
| 8) The figure below is formed by using a semi-circle and a quadrant. Find the perimeter and area of the shaded part, rounding your answers to the nearest whole number. π = 3.142
cm cm2 Answer:_______________ |
| 9) The figure below is formed by using a semi-circle and a quadrant. Find the perimeter and area of the shaded part, rounding your answers to the nearest whole number. π = 3.142
cm cm2 Answer:_______________ |
| 10) The figure below is formed by using a semi-circle and a quadrant. Find the perimeter and area of the shaded part, rounding your answers to the nearest whole number. π = 3.142
cm cm2 Answer:_______________ |
| 1) The figure below is formed by using a semi-circle and a quadrant. Find the perimeter and area of the shaded part, rounding your answers to the nearest whole number. π = 3.142
Answer: 107 cm Answer: 454 cm2 SOLUTION 1 : Step 1: Diameter of quarter circle → 2 x 34 cm = 68.000 cm Step 2: Circumference of quarter circle → x π x 68.000 cm = 53.414 cm Step 3: Circumference of semi circle → x π x 34 cm = 53.414 cm Step 4: Perimeter of shaded part → 53.414 cm + 53.414 cm + 34 cm = 106.828 cm ≈ 107 cm Step 5: Area of quarter cicle → x π x 34 cm x 34 cm = 908.038 cm2 Step 6 : Radius of semi circle → 34 cm ÷ 2 = 17 cm Step 7: Area of semi circle → x π x 17 cm x 17 cm = 454.019 cm2 Step 8: Area of shaded part → 908.038 cm2 - 454.019 cm2 = 454.019 cm2 ≈ 454 cm2 |
| 2) The figure below is formed by using a semi-circle and a quadrant. Find the perimeter and area of the shaded part, rounding your answers to the nearest whole number. π = 3.142
Answer: 50 cm Answer: 101 cm2 SOLUTION 1 : Step 1: Diameter of quarter circle → 2 x 16 cm = 32.000 cm Step 2: Circumference of quarter circle → x π x 32.000 cm = 25.136 cm Step 3: Circumference of semi circle → x π x 16 cm = 25.136 cm Step 4: Perimeter of shaded part → 25.136 cm + 25.136 cm + 16 cm = 50.272 cm ≈ 50 cm Step 5: Area of quarter cicle → x π x 16 cm x 16 cm = 201.088 cm2 Step 6 : Radius of semi circle → 16 cm ÷ 2 = 8 cm Step 7: Area of semi circle → x π x 8 cm x 8 cm = 100.544 cm2 Step 8: Area of shaded part → 201.088 cm2 - 100.544 cm2 = 100.544 cm2 ≈ 101 cm2 |
| 3) The figure below is formed by using a semi-circle and a quadrant. Find the perimeter and area of the shaded part, rounding your answers to the nearest whole number. π = 3.142
Answer: 63 cm Answer: 157 cm2 SOLUTION 1 : Step 1: Diameter of quarter circle → 2 x 20 cm = 40.000 cm Step 2: Circumference of quarter circle → x π x 40.000 cm = 31.42 cm Step 3: Circumference of semi circle → x π x 20 cm = 31.420 cm Step 4: Perimeter of shaded part → 31.42 cm + 31.420 cm + 20 cm = 62.840 cm ≈ 63 cm Step 5: Area of quarter cicle → x π x 20 cm x 20 cm = 314.200 cm2 Step 6 : Radius of semi circle → 20 cm ÷ 2 = 10 cm Step 7: Area of semi circle → x π x 10 cm x 10 cm = 157.100 cm2 Step 8: Area of shaded part → 314.200 cm2 - 157.100 cm2 = 157.100 cm2 ≈ 157 cm2 |
| 4) The figure below is formed by using a semi-circle and a quadrant. Find the perimeter and area of the shaded part, rounding your answers to the nearest whole number. π = 3.142
Answer: 75 cm Answer: 226 cm2 SOLUTION 1 : Step 1: Diameter of quarter circle → 2 x 24 cm = 48.000 cm Step 2: Circumference of quarter circle → x π x 48.000 cm = 37.704 cm Step 3: Circumference of semi circle → x π x 24 cm = 37.704 cm Step 4: Perimeter of shaded part → 37.704 cm + 37.704 cm + 24 cm = 75.408 cm ≈ 75 cm Step 5: Area of quarter cicle → x π x 24 cm x 24 cm = 452.448 cm2 Step 6 : Radius of semi circle → 24 cm ÷ 2 = 12 cm Step 7: Area of semi circle → x π x 12 cm x 12 cm = 226.224 cm2 Step 8: Area of shaded part → 452.448 cm2 - 226.224 cm2 = 226.224 cm2 ≈ 226 cm2 |
| 5) The figure below is formed by using a semi-circle and a quadrant. Find the perimeter and area of the shaded part, rounding your answers to the nearest whole number. π = 3.142
Answer: 113 cm Answer: 509 cm2 SOLUTION 1 : Step 1: Diameter of quarter circle → 2 x 36 cm = 72.000 cm Step 2: Circumference of quarter circle → x π x 72.000 cm = 56.556 cm Step 3: Circumference of semi circle → x π x 36 cm = 56.556 cm Step 4: Perimeter of shaded part → 56.556 cm + 56.556 cm + 36 cm = 113.112 cm ≈ 113 cm Step 5: Area of quarter cicle → x π x 36 cm x 36 cm = 1018.008 cm2 Step 6 : Radius of semi circle → 36 cm ÷ 2 = 18 cm Step 7: Area of semi circle → x π x 18 cm x 18 cm = 509.004 cm2 Step 8: Area of shaded part → 1018.008 cm2 - 509.004 cm2 = 509.004 cm2 ≈ 509 cm2 |
| 6) The figure below is formed by using a semi-circle and a quadrant. Find the perimeter and area of the shaded part, rounding your answers to the nearest whole number. π = 3.142
Answer: 57 cm Answer: 127 cm2 SOLUTION 1 : Step 1: Diameter of quarter circle → 2 x 18 cm = 36.000 cm Step 2: Circumference of quarter circle → x π x 36.000 cm = 28.278 cm Step 3: Circumference of semi circle → x π x 18 cm = 28.278 cm Step 4: Perimeter of shaded part → 28.278 cm + 28.278 cm + 18 cm = 56.556 cm ≈ 57 cm Step 5: Area of quarter cicle → x π x 18 cm x 18 cm = 254.502 cm2 Step 6 : Radius of semi circle → 18 cm ÷ 2 = 9 cm Step 7: Area of semi circle → x π x 9 cm x 9 cm = 127.251 cm2 Step 8: Area of shaded part → 254.502 cm2 - 127.251 cm2 = 127.251 cm2 ≈ 127 cm2 |
| 7) The figure below is formed by using a semi-circle and a quadrant. Find the perimeter and area of the shaded part, rounding your answers to the nearest whole number. π = 3.142
Answer: 126 cm Answer: 628 cm2 SOLUTION 1 : Step 1: Diameter of quarter circle → 2 x 40 cm = 80.000 cm Step 2: Circumference of quarter circle → x π x 80.000 cm = 62.84 cm Step 3: Circumference of semi circle → x π x 40 cm = 62.840 cm Step 4: Perimeter of shaded part → 62.84 cm + 62.840 cm + 40 cm = 125.680 cm ≈ 126 cm Step 5: Area of quarter cicle → x π x 40 cm x 40 cm = 1256.800 cm2 Step 6 : Radius of semi circle → 40 cm ÷ 2 = 20 cm Step 7: Area of semi circle → x π x 20 cm x 20 cm = 628.400 cm2 Step 8: Area of shaded part → 1256.800 cm2 - 628.400 cm2 = 628.400 cm2 ≈ 628 cm2 |
| 8) The figure below is formed by using a semi-circle and a quadrant. Find the perimeter and area of the shaded part, rounding your answers to the nearest whole number. π = 3.142
Answer: 119 cm Answer: 567 cm2 SOLUTION 1 : Step 1: Diameter of quarter circle → 2 x 38 cm = 76.000 cm Step 2: Circumference of quarter circle → x π x 76.000 cm = 59.698 cm Step 3: Circumference of semi circle → x π x 38 cm = 59.698 cm Step 4: Perimeter of shaded part → 59.698 cm + 59.698 cm + 38 cm = 119.396 cm ≈ 119 cm Step 5: Area of quarter cicle → x π x 38 cm x 38 cm = 1134.262 cm2 Step 6 : Radius of semi circle → 38 cm ÷ 2 = 19 cm Step 7: Area of semi circle → x π x 19 cm x 19 cm = 567.131 cm2 Step 8: Area of shaded part → 1134.262 cm2 - 567.131 cm2 = 567.131 cm2 ≈ 567 cm2 |
| 9) The figure below is formed by using a semi-circle and a quadrant. Find the perimeter and area of the shaded part, rounding your answers to the nearest whole number. π = 3.142
Answer: 88 cm Answer: 308 cm2 SOLUTION 1 : Step 1: Diameter of quarter circle → 2 x 28 cm = 56.000 cm Step 2: Circumference of quarter circle → x π x 56.000 cm = 43.988 cm Step 3: Circumference of semi circle → x π x 28 cm = 43.988 cm Step 4: Perimeter of shaded part → 43.988 cm + 43.988 cm + 28 cm = 87.976 cm ≈ 88 cm Step 5: Area of quarter cicle → x π x 28 cm x 28 cm = 615.832 cm2 Step 6 : Radius of semi circle → 28 cm ÷ 2 = 14 cm Step 7: Area of semi circle → x π x 14 cm x 14 cm = 307.916 cm2 Step 8: Area of shaded part → 615.832 cm2 - 307.916 cm2 = 307.916 cm2 ≈ 308 cm2 |
| 10) The figure below is formed by using a semi-circle and a quadrant. Find the perimeter and area of the shaded part, rounding your answers to the nearest whole number. π = 3.142
Answer: 82 cm Answer: 265 cm2 SOLUTION 1 : Step 1: Diameter of quarter circle → 2 x 26 cm = 52.000 cm Step 2: Circumference of quarter circle → x π x 52.000 cm = 40.846 cm Step 3: Circumference of semi circle → x π x 26 cm = 40.846 cm Step 4: Perimeter of shaded part → 40.846 cm + 40.846 cm + 26 cm = 81.692 cm ≈ 82 cm Step 5: Area of quarter cicle → x π x 26 cm x 26 cm = 530.998 cm2 Step 6 : Radius of semi circle → 26 cm ÷ 2 = 13 cm Step 7: Area of semi circle → x π x 13 cm x 13 cm = 265.499 cm2 Step 8: Area of shaded part → 530.998 cm2 - 265.499 cm2 = 265.499 cm2 ≈ 265 cm2 |